¿Cuanto saben tus alumnos de matemática? ponlos a prueba desafiándolos con este juego de preguntas y repuestas.
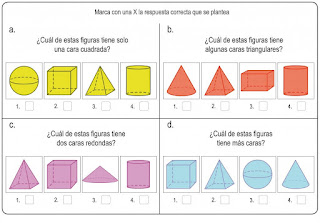
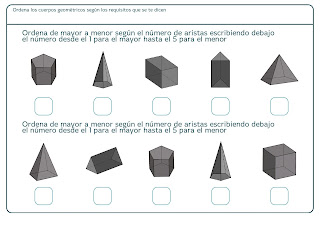
Figuras y cuerpos geométricos
Les dejo los moldes para imprimir y armar sus propio cuerpos geométricos
Problemas:
Manolo tiene 10 caramelos, Jaime el doble y Raúl tiene el triple que Jaime ¿Cuántos caramelos tienen entre los tres?
Datos. Solución
Respuesta: (Recordar que tiene que ser completa de modo que si no pudiera ver el enunciado del problema al leer la respuesta podría fácilmente imaginarlo)
---------------------------------------------------------------------------------Voy a casa en el autobús de las 16:30h. ¿A qué hora llegaré si el autobús realiza el recorrido en 15 minutos?
Datos. Solución
Respuesta:
--------------------------------------------------------------------------------------------------------------------------
En un jarrón hay 5 rosas y en otro el triple que en el primero. ¿Cuántas rosas hay entre los dos jarrones?
Datos. Solución
Respuesta:
--------------------------------------------------------------------------------------------------------------------------
En la clase de primero hay 37 alumnos y en la de segundo 39. Hoy han faltado a clase 12 alumnos de primero y 7 de segundo ¿Cuántos alumnos hemos ido hoy a clase?
Datos. Solución
Respuesta:
--------------------------------------------------------------------------------------------------------------------------
Jaime ha representado un gráfico de barras con el número de cromo que tienen sus amigos y él.
a) ¿Quién tiene más cromos de los tres?
Datos. Solución
Respuesta:
--------------------------------------------------------------------------------------------------------------------------
b) ¿Quién tiene menos cromos Jaime o Guillermo?
Datos. Solución
Respuesta:
--------------------------------------------------------------------------------------------------------------------------
c) ¿Cuántos cromos tiene más Jaime que Francisco?
Datos. Solución
Respuesta:
--------------------------------------------------------------------------------------------------------------------------
Para ir a la escuela, Juan pasa cada día por la plaza de la iglesia. Desde su casa a la plaza hay 125 metros y de la plaza a la escuela hay 250 metros. Si recorre este camino 4 veces al día. ¿Qué distancia caminará durante la semana?
Datos. Solución
Respuesta:
--------------------------------------------------------------------------------------------------------------------------
TARJETAS PARA PRACTICAR LA MULTIPLICACIÓN, LA DIVISIÓN Y LA DESCOMPOSICIÓN FACTORIAL
He visto una ingeniosa forma de practicar las tablas de multiplicar, la propiedad conmutativa de la multiplicación, la división o la factorización de un número. Y muy importante, pueden descubrir la relación entre la multiplicación y la división.
Se trata de unas tarjetas hexagonales donde hay tres números en cada una: dos de ellos multiplicados nos proporciona el tercer número, como puedes ver en la siguiente imagen

El número escrito en la parte inferior es el producto de los dos números sobre él. A partir de estos tres números los niños podrán hacer las siguientes relaciones:
- 9 x 7 = 63
- 7 x 9 = 63
- 7 = 63 : 9
- 9 = 63 : 7
Como ya te estarás imaginando, se pueden realizar varias preguntas a partir de estos tres números. Dependiendo de si estamos buscando el resultado de un producto o queremos hallar el resultado de la división o estamos buscando la descomposición de un número en dos factores. La caja sirve para ocultar un factor o el resultado del producto por lo que los niños pueden realizar la actividad de manera autónoma.
Una vez que tengas la caja, solo tendrás que colocar una pila de tarjetas y proponer al niño que diga el número que falta en la tarjeta. Después de responder, saca la tarjeta y comprueba su respuesta, así la actividad es autocorrectiva.
A continuación podes ver ejemplos a partir de la tarjeta que contiene 3, 5 y 15.

Primer y segundo ejemplos: dado un factor y el resultado, hallar el otro factor.
En estos casos «escondemos» un factor. La posibles preguntas son:
- Un número desconocido multiplicado por 5 nos da 15. ¿Cuál es ese número?
- ¿Por cuánto tenemos que multiplicar 5 para obtener 15?
- ¿Cuánto es 15 dividido entre 5?
Tercer ejemplo: dados dos factores, buscar su resultado.
Ahora escondemos el resultado del producto:
- ¿Cuánto es tres veces cinco?
- ¿Cuánto nos da cinco veces tres?
- ¿Qué número dividido entre 5 nos da 3?
- ¿Qué número dividido entre 3 nos da 5?
Cuarto ejemplo: dado un número, encontrar dos números que multiplicados den el primero.
En este ejemplo solo mostramos el resultado de la multiplicación.
- Encuentra dos números que multiplicados te den 15.
Observa que en este caso la solución no es única, ya que existen diferente factorizaciones. Si no tenemos en cuenta el orden (es decir, es lo mismo 3 x 5 que 5 x 3), en este ejemplo solo hay una posible solución pero en otros casos como 12, encontraríamos dos soluciones: 3 x 4 y 2 x 6.
¿Viste que atractivo es usar materiales manipulable para que los estudiantes afiancen la multiplicación? ¿Trabajas la multiplicación a través del juego? ¿Te gusta la idea?
Aquí tienes un ejemplo de una ficha de multiplicaciones
Me gusta la idea de que sea una ficha autocorrectora (el niño ve si lo ha hecho bien por el dibujo), no tanto lo de colorea el dibujo, pero en conjunto es interesante que el trabajo de matemáticas de afianzar cálculos tenga un componente lúdico
A partir de este modelo podes crear todo lo que tu imaginación te permita.¡Animate!
Afiches para el aula: INFOGRAFÍAS
JUEGO-TABLERO PARA PRACTICAR LAS TABLAS DE MULTIPLICAR
Cualquier juego que ayude a los niños a familiarizarse con las tablas de multiplicar a través de la diversión es bienvenido, ¿verdad? Ya sé que en el blog puedes encontrar varios juegos que tienen la misma finalidad, pero siempre se tienen que buscar recursos nuevos, para hacer el aprendizaje más ameno.
MATERIAL
- cartulina para hacer un tablero.
- cartulina para hacer las cartas de las multiplicaciones (mejor si son de colores distintos).
- velcro para pegar las cartas
- plastificadora
CÓMO CONSTRUIR EL JUEGO PARA PRACTICAR LAS TABLAS DE MULTIPLICAR
Primeramente tienes que crear el tablero del juego, tal y como lo ves en la foto siguiente.
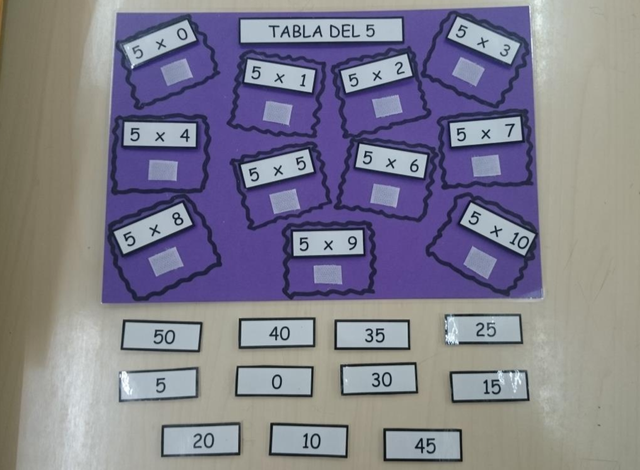
A continuación recorta las tarjetas y escribe en ellas las multiplicaciones y los resultados correspondientes.
Puedes hacer todas las tablas de multiplicar o sólo aquellas con la que estés trabajando ahora mismo.
Para que no se rompa fácilmente cuando lo utilicéis varias veces, te recomiendo que lo plastifiques. Así será más duradero en el tiempo.
Además, para que sea más práctico de jugar y las tarjetas no se muevan, lo mejor es pegar un pequeño velcro detrás de cada tarjeta y en cada uno de los espacios que hay en el tablero.
CÓMO JUGAR CON EL TABLERO
La verdad es que el tablero ofrece una gran cantidad de posibilidades de juego.
Aquí te voy a mostrar 4 de ellas, pero estoy segura de que se te ocurrirán más ideas aún.
Actividad 1
Para empezar a practicar una tabla en concreto lo que puedes hacer es pegar en el tablero todas las multiplicaciones de la tabla que quieres practicar y darles a ellos los resultados, que tendrán que pegar en el lugar correspondiente.
Actividad 2
Cuando ya tengan un poco de destreza con las multiplicaciones y los resultados, puedes hacer el juego al revés. En el tablero pega solamente las tarjetas con las soluciones y ellos tendrán que enganchar la multiplicación correspondiente a cada resultado.
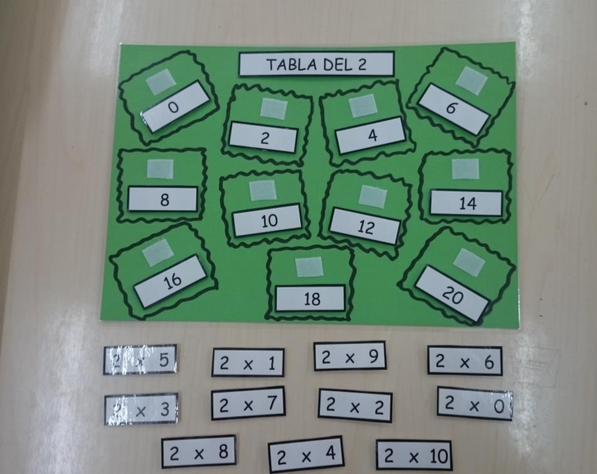
Actividad 3
Otra idea es mezclar las tablas de multiplicar y realizar una de las dos opciones anteriores, sin centrarse en una tabla en concreto.
Actividad 4
Ya cuando hayan trabajado todas las tablas, puedes mezclar en el tablero multiplicaciones de varias tablas, poner resultados y poner multiplicaciones. ¡Esto sí que será divertido!
Ideas para material didáctico:
Muy interesante forma de multiplicar sin saber de memoria las tablas
Hola!!! encontré un video de un colega que explica con lujo de detalles este sisitema de multiplicación que me encantó
y como estaba con el tema de multiplicar me preguntaba si en la mayoría de lo países han dejado de esperar que los niños aprendan de memoria las diez tablas y les dan estrategias para resolver y saltar semejante dificultad... porqué no hacerlo nosotros también.
Acá les dejo otro video donde se explican los distintos métodos de multiplicar sin saber las tablas, está muy bueno para practicarlo y dedicar una clase completa a explorar con los niños los diferentes métodos.
Bueno les dejo la inquietud hay que practicar un poco y les aseguro que los niños jamás volverán a tener dificultades para multiplicar.
Y para los más chiquitos también podemos proponer el juego de las manos, es muy estimulante para sus mentes en crecimiento, los lleva por el camino del cálculo mental y los ayuda a desarrollar mayor capacidad de deducción.
Hasta pronto!!!
Hoy hablemos de geometría les dejo este PDF
Estrategias didacticas Tiene muchas propuestas para las clases en primer ciclo de geometría
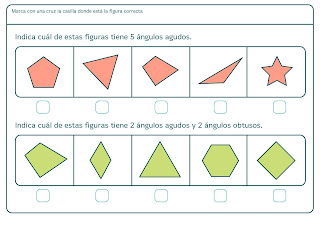
Veamos algunas propuestas de ángulos
Propuestas de ejercitación:
Olimpíada Matemática
(EJERCICIOS DE PRÁCTICA)
Primer Nivel
1-
Todas las semanas, Matías recibe una cuota para sus gastos.
Una semana ahorra la mitad de la cuota de esa semana, la semana siguiente ahorra la cuarta parte de la cuota de esa semana.
Así va alternando: una semana ahorra la mitad y la siguiente semana ahorra la cuarta parte.
De este modo, en 48 semanas ahorra $ 288. ¿Cuál es su cuota semanal?
Todas las semanas, Matías recibe una cuota para sus gastos.
Una semana ahorra la mitad de la cuota de esa semana, la semana siguiente ahorra la cuarta parte de la cuota de esa semana.
Así va alternando: una semana ahorra la mitad y la siguiente semana ahorra la cuarta parte.
De este modo, en 48 semanas ahorra $ 288. ¿Cuál es su cuota semanal?
2-
Un
sobre rectangular, abierto tiene 82 cm de perímetro; cerrado su
perímetro es de 80 cm.
La solapa es triangular y tiene 50 cm de perímetro.
Indica cuánto miden los lados del sobre y los de la solapa.
La solapa es triangular y tiene 50 cm de perímetro.
Indica cuánto miden los lados del sobre y los de la solapa.
3-
Pedro tiene 15 cubos de madera, todos iguales.
Usando todos los cubos, arma y desarma torres en las que cada piso tiene una sola fila de cubos.
Si cada piso tiene menos cubos que el anterior, indica, para cada torre, cuántos cubos hay en cada piso. Da todas las posibilidades.
Pedro tiene 15 cubos de madera, todos iguales.
Usando todos los cubos, arma y desarma torres en las que cada piso tiene una sola fila de cubos.
Si cada piso tiene menos cubos que el anterior, indica, para cada torre, cuántos cubos hay en cada piso. Da todas las posibilidades.
4-
Todas las semanas, Matías recibe una cuota para sus gastos.
Una semana ahorra la mitad de la cuota de esa semana, la semana siguiente ahorra la tercera parte de la cuota de esa semana y la siguiente, ahorra la cuarta parte de la cuota de esa semana.
Así va alternando: una semana ahorra la mitad, la siguiente semana ahorra la tercera parte y la siguiente, ahorra la cuarta parte.
De este modo, en 48 semanas ahorra $ 312. ¿Cuál es su cuota semanal?
Todas las semanas, Matías recibe una cuota para sus gastos.
Una semana ahorra la mitad de la cuota de esa semana, la semana siguiente ahorra la tercera parte de la cuota de esa semana y la siguiente, ahorra la cuarta parte de la cuota de esa semana.
Así va alternando: una semana ahorra la mitad, la siguiente semana ahorra la tercera parte y la siguiente, ahorra la cuarta parte.
De este modo, en 48 semanas ahorra $ 312. ¿Cuál es su cuota semanal?
5-
Un sobre rectangular, abierto tiene 82 cm de perímetro; cerrado su perímetro es de 80 cm.
La solapa es triangular y tiene 50 cm de perímetro.
Un sobre rectangular, abierto tiene 82 cm de perímetro; cerrado su perímetro es de 80 cm.
La solapa es triangular y tiene 50 cm de perímetro.
Indica cuánto miden los lados del sobre y los de la solapa.
6-
Pedro tiene 15 cubos de madera, todos iguales.
Usando todos los cubos, arma y desarma torres en las que cada piso tiene una sola fila de cubos.
Si cada piso tiene menos cubos que el anterior, indica, para cada torre, cuántos cubos hay en cada piso. Da todas las posibilidades.
Pedro tiene 15 cubos de madera, todos iguales.
Usando todos los cubos, arma y desarma torres en las que cada piso tiene una sola fila de cubos.
Si cada piso tiene menos cubos que el anterior, indica, para cada torre, cuántos cubos hay en cada piso. Da todas las posibilidades.
Acá les dejo una recopilación en pdf listo para descargar e imprimir de ejercicios para practicar con sus alumnos de primer nivel ejercicios de antiguas olimpiadas
Segundo Nivel
1-
Los chicos de quinto, sexto y séptimo grados quieren ir juntos de excursión.
En quinto grado hay 30 chicos; en sexto, 25 y en séptimo, 20.
La excursión se puede hacer en micros de 50 asientos o de 30 asientos.
La empresa cobra tantos pasajes como asientos tiene el micro, aunque no se ocupen todos.
Si usan dos micros de 50 asientos y dividen el gasto en partes iguales, cada chico debe pagar $20.
Si usan un micro de 50 asientos y uno de 30 asientos y dividen el gasto en partes iguales, a cada uno le tocará pagar $ 18.
¿Cuánto cuesta cada pasaje en el micro de 30 asientos?
Los chicos de quinto, sexto y séptimo grados quieren ir juntos de excursión.
En quinto grado hay 30 chicos; en sexto, 25 y en séptimo, 20.
La excursión se puede hacer en micros de 50 asientos o de 30 asientos.
La empresa cobra tantos pasajes como asientos tiene el micro, aunque no se ocupen todos.
Si usan dos micros de 50 asientos y dividen el gasto en partes iguales, cada chico debe pagar $20.
Si usan un micro de 50 asientos y uno de 30 asientos y dividen el gasto en partes iguales, a cada uno le tocará pagar $ 18.
¿Cuánto cuesta cada pasaje en el micro de 30 asientos?
2-
En
la figura:
C es un cuadrado, T es un triángulo rectángulo y U es un triángulo isósceles rectángulo.
El área de U es 800 cm2.
El área de C es el triple del área de T.
C es un cuadrado, T es un triángulo rectángulo y U es un triángulo isósceles rectángulo.
El área de U es 800 cm2.
El área de C es el triple del área de T.
¿Cuál es el área de toda la figura?
3-
Ana escribe un número de 4 cifras.
Bea escribe el siguiente del número que escribió Ana.
La suma de los dígitos del número que escribió Ana es 25.
La suma de los dígitos del número que escribió Bea es 17.
¿Qué número pudo haber escrito Ana?
Da todas las posibilidades.
4-
Los chicos de quinto, sexto y séptimo grados quieren ir juntos de excursión.
En quinto grado hay 30 chicos; en sexto, 25 y en séptimo, 20.
La excursión se puede hacer en micros de 50 asientos o de 30 asientos.
La empresa cobra tantos pasajes como asientos tiene el micro, aunque no se ocupen todos.
Si usan dos micros de 50 asientos y dividen el gasto en partes iguales, cada chico debe pagar $20.
Si usan un micro de 50 asientos y uno de 30 asientos y dividen el gasto en partes iguales, a cada uno le tocará pagar $ 18.
¿Cuánto cuesta cada pasaje en el micro de 30 asientos?
Ana escribe un número de 4 cifras.
Bea escribe el siguiente del número que escribió Ana.
La suma de los dígitos del número que escribió Ana es 25.
La suma de los dígitos del número que escribió Bea es 17.
¿Qué número pudo haber escrito Ana?
Da todas las posibilidades.
4-
Los chicos de quinto, sexto y séptimo grados quieren ir juntos de excursión.
En quinto grado hay 30 chicos; en sexto, 25 y en séptimo, 20.
La excursión se puede hacer en micros de 50 asientos o de 30 asientos.
La empresa cobra tantos pasajes como asientos tiene el micro, aunque no se ocupen todos.
Si usan dos micros de 50 asientos y dividen el gasto en partes iguales, cada chico debe pagar $20.
Si usan un micro de 50 asientos y uno de 30 asientos y dividen el gasto en partes iguales, a cada uno le tocará pagar $ 18.
¿Cuánto cuesta cada pasaje en el micro de 30 asientos?
En
la figura:
C es un cuadrado, R un rectángulo, T es un triángulo rectángulo y U es un triángulo isósceles rectángulo.
El área de U es 800 cm2.
El área de C es el doble del área de R.
El área de T es igual al área de R.
¿Cuál es el área de toda la figura?
C es un cuadrado, R un rectángulo, T es un triángulo rectángulo y U es un triángulo isósceles rectángulo.
El área de U es 800 cm2.
El área de C es el doble del área de R.
El área de T es igual al área de R.
¿Cuál es el área de toda la figura?
6-
Ana escribe un número de 4 cifras.
Bea escribe el siguiente del número que escribió Ana.
La suma de los dígitos del número que escribió Ana es 25.
La suma de los dígitos del número que escribió Bea es 17.
¿Qué número pudo haber escrito Ana?
Da todas las posibilidades.
Acá les dejo una recopilación en pdf listo para descargar e imprimir de ejercicios para practicar con sus alumnos de segundo nivel de antiguas olimpiadas
Ana escribe un número de 4 cifras.
Bea escribe el siguiente del número que escribió Ana.
La suma de los dígitos del número que escribió Ana es 25.
La suma de los dígitos del número que escribió Bea es 17.
¿Qué número pudo haber escrito Ana?
Da todas las posibilidades.
Acá les dejo una recopilación en pdf listo para descargar e imprimir de ejercicios para practicar con sus alumnos de segundo nivel de antiguas olimpiadas
Tercer Nivel
1-
En diciembre del año pasado, las tres cuartas partes de los alumnos inscriptos en la escuela, eran varones.
La inscripción se reanudó en febrero; se agregaron 105 varones y 195 mujeres.
El número de mujeres representaba, a fin de febrero, la tercera parte de los inscriptos hasta ese momento.
¿Cuántas mujeres había inscriptas en diciembre?
En diciembre del año pasado, las tres cuartas partes de los alumnos inscriptos en la escuela, eran varones.
La inscripción se reanudó en febrero; se agregaron 105 varones y 195 mujeres.
El número de mujeres representaba, a fin de febrero, la tercera parte de los inscriptos hasta ese momento.
¿Cuántas mujeres había inscriptas en diciembre?
2-
En la circunferencia de centro O,
En la circunferencia de centro O,
- los arcos EF, FG y GE son iguales, cada uno de 25,12 cm de longitud,
- el arco GH es igual al arco HE.
¿Cuál es el área de EFGH?
3-
Juan escribe una lista de 15 números en la que:
- el cuarto número es 5,
- el décimo número es 10,
- el último número es 22,
- siempre que se suman cuatro números consecutivos de la lista, se obtiene 215.
Juan escribe una lista de 15 números en la que:
- el cuarto número es 5,
- el décimo número es 10,
- el último número es 22,
- siempre que se suman cuatro números consecutivos de la lista, se obtiene 215.
¿Cuál
es la lista de números que escribió Juan?
4-
En diciembre del año pasado, las tres cuartas partes de los alumnos inscriptos en la escuela, eran varones.
La inscripción se reanudó en febrero; se agregaron 105 varones y 195 mujeres.
El número de mujeres representaba, a fin de febrero, la tercera parte de los inscriptos hasta ese momento.
¿Cuántas mujeres había inscriptas en diciembre?
5-
Sobre una circunferencia de centro O, se marcan los puntos E,F,G y H de modo que los arcos GH y HE son iguales,
los arcos EF y FG son ambos iguales al doble del arco GH.
En diciembre del año pasado, las tres cuartas partes de los alumnos inscriptos en la escuela, eran varones.
La inscripción se reanudó en febrero; se agregaron 105 varones y 195 mujeres.
El número de mujeres representaba, a fin de febrero, la tercera parte de los inscriptos hasta ese momento.
¿Cuántas mujeres había inscriptas en diciembre?
5-
Sobre una circunferencia de centro O, se marcan los puntos E,F,G y H de modo que los arcos GH y HE son iguales,
los arcos EF y FG son ambos iguales al doble del arco GH.
La longitud del arco EF es 25,12 cm. El
punto A está alineado con F y G.
El punto D está alineado con F y E.
ABHG y CDEH son cuadrados.
El triángulo BCH es equilátero.
¿Cuál es el área de ABCDF?
ABHG y CDEH son cuadrados.
El triángulo BCH es equilátero.
¿Cuál es el área de ABCDF?
6-
Juan escribe una lista de 17 números enteros en la que:
- algún número es el doble de otro,
- el cuarto número es 5,
- el décimo número es 30,
- el último número es 21,
- siempre que se suman cinco números consecutivos de la lista, se obtiene 215.
¿Cuál es la lista de números que escribió Juan?
¿Hay más de una? En caso afirmativo, da todas las posibles.
Juan escribe una lista de 17 números enteros en la que:
- algún número es el doble de otro,
- el cuarto número es 5,
- el décimo número es 30,
- el último número es 21,
- siempre que se suman cinco números consecutivos de la lista, se obtiene 215.
¿Cuál es la lista de números que escribió Juan?
¿Hay más de una? En caso afirmativo, da todas las posibles.
------------------------------------------------------------------------------------------
Hoy tengo para recomendarles una página que me pareció ¡muy buena!
Allí encontrarán una lista de las competencias de matemáticas para los estudiantes de preescolar a sexto grado. Estas competencias están clasificadas en categorías: situando el cursor sobre el nombre de una competencia y haciendo click sobre la misma, se abrirá una nueva ventana y comenzarán los ejercicios. Cada alumno o alumna deberá tener su propio usuario para salir al finalizar el tiempo de clase y volver a entrar al mismo lugar donde dejó la siguiente vez- IXL llevará un seguimiento de sus puntuaciones y las preguntas irán aumentando de dificultad según vayan mejorando.¿No es buenísimo?
Podes trabajar con tus alumnos cada uno con su dispositivo o (si la escuela lo tiene) en la sala de informática
-----------------------------------------------------------------------------
Les dejo acá fichas para usar con primer grado ¡¡espero que les sea útil!!
CÁLCULO
COMPARACIONES
------------------------------------------------------------------




------------------------------------------------------------------
(PRÓXIMAMENTE FICHAS PARA CUARTO GRADO)
------------------------------------------------------------------
MATERIAL E INFORMACIÓN PARA ENSEÑAR FRACCIONES
Les dejo acá fichas para usar con primer grado ¡¡espero que les sea útil!!
CÁLCULO
"MAYOR QUE..." Y "MENOR QUE..."
NÚMEROS NATURALES HASTA LA CENTENA
ORDENAR DE MENOR A MAYOR Y DE MAYOR A MENOR
ORDINALES
SUMAS Y RESTAS
VALOR POSICIONAL
MATERIAL EN FORMATO PDF PARA DESCARGAR Y PODER IMPRIMIR
MAGNITUDES
COMPARAR CANTIDADES
COMPARAR TAMAÑOS Y LONGITUDES
UNIDADES DE TIEMPO
DINERO
GEOMETRÍA POSICIONES Y MOVIMIENTOS
LINEAS
FIGURAS
CUERPOS
---------------------------------------------------------------------------
FICHAS PARA 2°GRADO PRIMARIA
GEOMETRÍA
Este es un cuadernillo muy simple para descargar en formato PDF listo para imprimir y usar. Cuadernillo geometria 1° y 2° grado
La geometría (del
latín geometrĭa, que proviene del idioma
griego γεωμετρία, geo tierra y metria medida),
es una rama de la matemática que se ocupa del estudio de las
propiedades de las figuras en el plano o el espacio, incluyendo: puntos, rectas, planos, politopos (que
incluyen paralelas, perpendiculares, curvas, superficies, polígonos, poliedros,
etc.).
Es la base
teórica de la geometría descriptiva o del dibujo técnico.
También da fundamento a instrumentos como el compás, el teodolito,
el pantógrafo o el sistema de posicionamiento global (en
especial cuando se la considera en combinación con el análisis
matemático y sobre todo con las ecuaciones diferenciales).
Sus
orígenes se remontan a la solución de problemas concretos relativos a medidas.
Tiene su
aplicación práctica en física aplicada, mecánica, arquitectura,
cartografía, astronomía, náutica, topografía, balística, etc.
Es útil en
la preparación de diseños e incluso en la elaboración de artesanía.
Las
matemáticas son una parte esencial en el aprendizaje de los niños ya que le
ayuda a desarrollar sus habilidades de razonamiento y resolución de problemas.
El cerebro viene programado para aprender y
utilizar conceptos matemáticos y los niños desde que empiezan a gatear
comienzan a explorar su entorno, manejando objetos y observando los diferentes
tamaños de sus juguetes.
En este enlace pueden encontrar juegos online de tangram excelente para geometría Tangram juegos online
FICHAS DE NUMERACIÓN
APROXIMACIÓN
ORDENAR NÚMEROS
ORDINALES
NÚMEROS PARES E IMPARES
VALOR POSICIONAL
OPERACIONES: SUMAS, RESTAS Y MULTIPLICACIÓN
(SIN SALIR DE ESTA PÁGINA SUBIENDO PODES ENCONTRAR RECURSOS PARA ENSEÑAR A MULTIPLICAR)
MAGNITUDES
PESO
CAPACIDAD
LONGITUD
EL TIEMPO, RELOJES ANALÓGICOS Y DIGITALES
SISTEMA MONETARIO
------------------------------------------------------------------
FICHAS PARA TRABAJAR NUMERACIÓN EN 3°GRADO DE PRIMARIA
NUMEROS
ORDENAR LOS NÚMEROS DE MENOR A MAYOR
O DE MAYOR A MENOR
MAYOR QUE.... O MENOR QUE....
NÚMEROS IMPARES Y PARES
VALOR POSICIONAL
SERIES NUMÉRICAS
MAGNITUDES
LONGITUD
CAPACIDAD
MASA
TIEMPO
RELOJES
GEOMETRÍA
UNA HERMOSA EXPERIENCIA CON MIS ALUMNOS FUE ARMAR CADA UNO SU PROPIA CAJA DE GEOMETRÍA CON DIFERENTES MATERIALES, CADA UNO TRABAJÓ CON LO QUE IBA CONSIGUIENDO Y LOS QUE TERMINARON PRIMERO AYUDARON A LOS REZAGADOS. ARMARON CAJAS Y LAS DECORARON A SU GUSTO CADA UNO LA SUYA.
EL OTRO DÍA ENCONTRÉ A UN EXALUMNO Y A LAS CARCAJADAS ME CONTÓ QUE SU HIJO ESTÁ USANDO LA CAJA QUE EL FABRICÓ CUANDO ME TUVO EN TERCER GRADO.... LAS BUENAS PRÁCTICAS SON PARA COMPARTIR Y MULTIPLICAR!!




------------------------------------------------------------------
MATERIAL E INFORMACIÓN PARA ENSEÑAR FRACCIONES
¿QUÉ ES UNA FRACCIÓN?
Fraccionar es dividir algo en partes, por tanto una fracción en matemáticas es dividir un número entero en partes iguales, por ejemplo dividimos un pastel en 3 partes y de ellas tomamos una, podemos decir que estamos cogiendo un tercio del pastel, una de tres partes. Se representa 1/3
TÉRMINOS DE UNA FRACCIÓN
La fracción está formada por dos términos: el numerador y el denominador . El numerador es el número que está sobre la linea de fracción y el denominador es el que está bajo la linea de fracción.
Vamos a aprender a leer fracciones: veamos un ejemplo
En la figura tenemos una circunferencia dividida en 8 partes, sombreadas en verde tenemos dos partes, luego el número fraccionario sería 2/8 y se lee dos octavos, dos partes de ocho. la solución por tanto es la tercer fracción presentada en la imagen.
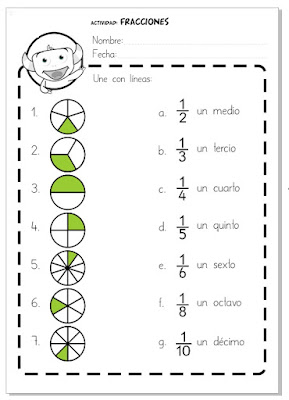
¿Es sencillo no? voy a dejarte ejercicio para que puedas utilizar en tus clase.





























































































































































































































































































































































































































































































































































































No hay comentarios:
Publicar un comentario